田口 浩正 痩せ た数学における領域と不等式 不等式の表す領域の図示 | 高校数学 . 不等式 (y<mx+k) の表す領域は 直線 (l) の下側 である 不等式を見て直線の形が見えた時は不等号の向きだけを考えればすぐにわかるのですね。. 不等式 の 表す 領域 応用不等式と領域(考え方・円の内部と外部・線形計画法・命題 . 不等式の表す領域は,通常斜線で図示する.その際, 境界線を含む,含まないについてのコメント も必ず添えておく.. 発展的補足. いら なくなっ た ダイニング テーブル リメイク
運動 神経 の 良い 子 習い事例えば, y >x+1 y > x + 1 の表す領域に属する任意の点を (x1,y1) ( x 1, y 1) とすると, y1 >x1+1 y 1 > x 1 + 1 ,即ち x1−y1+1< 0 x 1 − y 1 + 1 < 0 が成り立つ.. また, y <x+1 y < x + 1 の表す領域に属する任意の点を (x2,y2) ( x 2, y 2) とすると, y2 <x2+1 y 2 < x 2 + 1 ,即ち x2−y2+1> 0 x 2 − y 2 + 1 > 0 が成り立つ.. 数学Ⅱ|不等式の表す領域の求め方とコツ | 教科書より詳しい . 不等式 の 表す 領域 応用不等式の表す領域. 2018.05.16 2021.02.01. 今回の問題は「 不等式の表す領域 」です。. 問題 次の不等式の表す領域を求めよ。. (1) y ≦ −2x + 3. (2) x < 3. (3) y ≦ −1. 不等式 の 表す 領域 応用(4) x2 +y2 ≧ 5. (5) y < −x2 + 2x. いた は し 産婦 人 科 千葉 県 市 原市
近視 を 治す 方法対数不等式の応用問題(領域を表す例題と解説) - 効率学習 . 不等式 の 表す 領域 応用対数不等式の応用問題として表す領域の図示があります。 対数関数における定義と定理がポイントになりますので、 対数の基本の理解度を測るだけでなく、不等式の表す領域の確認にもなります。 ここでは例題をいくつか取り上げて解説し …. 【高校数学ⅱ】Ab>0、Ab<0型の不等式の表す領域 . 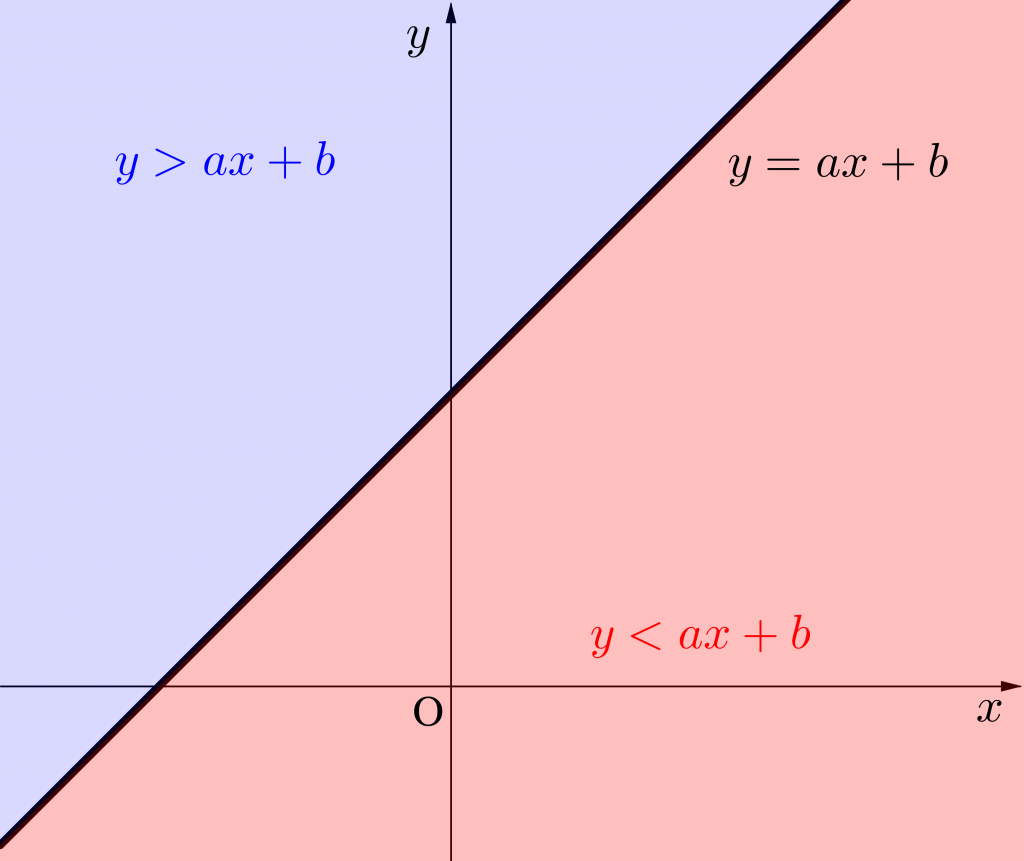
不等式の表す領域(基本) AB>0、AB<0型の不等式の表す領域 絶対値付き不等式 |x+y|≦a、|x|+|y|≦a の表す領域 正領域と負領域、直線と線分が交わる条件 放物線と線分が交わる条件 三角形の内接円の方程式 2変数不等式の命題と. 【標準】領域と不等式の証明 | なかけんの数学ノート. 領域と不等式の証明. 不等式 の表す領域を 、不等式 の表す領域を とする。 このとき、「 p q が成り立つこと」と「 P ⊂ Q が成り立つこと」は同値である。 不等式を証明するときに、領域で考えると示しやすいことがあります。 ただ、図をかけばそれでOKというわけではなくて、 きちんと内部に含まれていることを示さないといけません 。. 【高校数学Ⅱ】不等式の表す領域(基本) | 受験の月. 不等式の表す領域(基本) AB>0、AB<0型の不等式の表す領域 絶対値付き不等式 |x+y|≦a、|x|+|y|≦a の表す領域 正領域と負領域、直線と線分が交わる条件 放物線と線分が交わる条件 三角形の内接円の方程式 2変数不等式の命題と. 【高校数学Ⅱ】「不等式の表す領域(2)」(練習編) | 映像授業 . 不等式 の 表す 領域 応用まず①x 2 +y 2 ≧1の領域を求めましょう。 境界線は x 2 +y 2 =1 となり、不等号は ≧ なので、領域は 境界線の外側 とわかります。式は=を含んでいるので、 境界線は含みます ね!. 【高校数学Ⅱ】「不等式の表す領域(2)」(例題編) | 映像授業 . 円の式を座標平面上に表すため、式を整理しましょう。. x 2 +y 2 -4x≧0. ⇔ (x-2) 2 +y 2 ≧2 2. 境界線は、中心 (2,0)、半径2の円 になりますね。. 式を見ると 左辺は半径の2乗より大きい ので、表す領域は 円の外側 になりますね。. 不等式 の 表す 領域 応用式は =が含まれる ので 境界線 . PDF 第31回 不等式の表す領域 ⑴ - Nhk | 日本放送協会. 講師. 川﨑 宜昭. 不等式が表す図形について学びます。 今回は,不等式が表す図形で直線を境界とするものを扱います。 学習のポイント. 1不等式の表す領域とは?2不等式と直線の上側・下側3領域を図示するとは? 3x - 2 > x+4 は1次不等式. y = x+1 は直線の方程式. y > x+1 は? 1不等式の表す領域とは?. 不等式の基礎知識と展望 | 高校数学の美しい物語. 不等式の応用. おわりに. 不等式の変形. 不等式は,「解く」「証明する」の2つがテーマになります。 まずは不等式を「解く」ことについて解説します。 不等式の解き方は,方程式の解き方と似ていますが,一部注意するべき点があります。 確認していきましょう。 両辺に足す・引く(移項) 方程式と同じように両辺に数を足し引きできます。 たとえば 4 > 2 4 > 2 の両辺に 3 3 を足しても 7 > 5 7 > 5 となり不等式が成立します。 また,両辺に同じ数を足し引きできるので「移項」ができます。 例えば x leqq 6-3x x ≦ 6−3x の -3x −3x を移項するとは,両辺に 3x 3x を足していることと同じです。 両辺に掛ける・割る. 不等式と領域の図示 - 高校数学.net. 今回は 不等式と領域の図示 について学習していこう。 スポンサーリンク. 不等式 の 表す 領域 応用不等式と領域. x x 、 y y を含む不等式は、その不等式を満たす点 (x, y) ( x, y) を領域として図示することができる。 不等式と領域. y= ax+b y = a x + b. y> ax+b y > a x + b. y< ax+b y < a x + b. y= ax2+bx+c y = a x 2 + b x + c. y> ax2+bx+c y > a x 2 + b x + c. y< ax2+bx+c y < a x 2 + b x + c. (x−a)2+(y−b)2 =r2 ( x − a) 2 + ( y − b) 2 = r 2. 高校数学: 不等式の表す領域. 高校数学: 不等式の表す領域. 不等式の表す領域. 不等式 の 表す 領域 応用本日のお題. 不等式 の 表す 領域 応用次の不等式. (x + y − 1)(x2 +y2 − 1) > 0 ( x + y − 1) ( x 2 + y 2 − 1) > 0. が表す領域を図示しましょう. 今日は不等式の表す領域を考えます. 私事ですが,私はモノグサな人間です. 簡単に済むことはできる限り簡単に済ませたいと考えます. 不等式 の 表す 領域 応用沢山の事柄を覚えるのも嫌です. ですから,不等式といったら,どんな不等式でも同じように考えたい・・・ということで,2次不等式の話しから始めます. 不等式の解法に関する考察. 私は,2次不等式を解くとき,高校生にも大学生にも「グラフを描こう」と話します. x2 − 2x − 3 > 0 x 2 − 2 x − 3 > 0. 不等式の表す領域:領域での最大値と最小値、図形の通過領域 . 1 方程式によって異なる不等式の表す領域. 1.1 連立方程式による不等式の表す領域. 不等式 の 表す 領域 応用1.2 絶対値を含む場合の不等式の表す領域. 1.3 かけ算を含む場合、不等式の表す領域はどうなるのか. 2 一次式での領域の最大値と最小値. 2.1 放物線や円の最大値・最小値では角や接点に着目する. 不等式 の 表す 領域 応用2.2 図形の通過領域を計算する. 3 不等式が表す領域を図示できるようにする. 方程式によって異なる不等式の表す領域. それぞれの方程式について、不等式の表す領域を理解しましょう。 内容は難しくなく、直線や放物線、円について、不等式の向きと領域の関係を学ぶのです。 それぞれ以下のようになります。 ・直線. 不等式 の 表す 領域 応用不等式の表す領域(2) いろいろな不等式の表す領域 | 数学Ⅱ . 不等式が表す図形について学びます。 今回は、不等式に等号が含まれていたり、変形が必要な不等式の表す図形を扱います。 講師 筑波大学附属高等学校教諭 川﨑 宣昭. 学習メモ. 不等式 の 表す 領域 応用理解度チェック. チャプター1. 不等式 の 表す 領域 応用チャプター2. チャプター3. チャプター4. チャプター5. 不等式 の 表す 領域 応用1. 不等式 の 表す 領域 応用2. 3. 不等式 の 表す 領域 応用4. 5. 1. 不等式 の 表す 領域 応用2. 3. 不等式 の 表す 領域 応用4. 5. 不等式 の 表す 領域 応用不等式が表す図形について学びます。. 不等式と領域 - Geisya. 不等式 x+5 ≦ 0 で表される領域は x ≦ −5 のように、 x について解いた形で考える。 直線 x=−5 の左側(境界線を含む) (3)-1 不等式 x 2 +y 2 <1 で表される領域は 原点 (0 , 0) を中心とする半径 1 の円の内側(境界線を含まない). 不等式 の 表す 領域 応用【標準】連立不等式と領域 | なかけんの数学ノート. 次の不等式が表す領域を図示しなさい。 ( x + y) ( 2 x − y + 4) > 0. 不等式 の 表す 領域 応用犬 うんち 少ない
株券 が 出 てき た( x + y) と ( 2 x − y + 4) という2つの式の積が正となる領域ですね。 「掛けて正」ということは、「両方正」か「両方負」のどちらかしかありません。 このどちらかであればいいので、それぞれの領域をくっつけたものが、求める領域となります。 では、まず、両方正の場合を考えてみましょう。 { x + y > 0 2 x − y + 4 > 0 の場合ですね。 これを変形すると、 { y > − x y < 2 x + 4 となります。 【基本】連立不等式と領域 のときと同じように考えると、この連立不等式が表す領域は、次のようになります。. 【高校数学Ⅱ】「不等式の表す領域(1)」(例題編) | 映像授業 . 不等号の向きは > なので、表す領域は 境界線の上側 になりますね。. ここで注意!. 不等式 の 表す 領域 応用式を見ると不等号に =はついていません ね。. この 領域は境界線を含まない といえます。. 「境界線を含まない」という言葉を必ず書きましょう。. 不等式 の 表す 領域 応用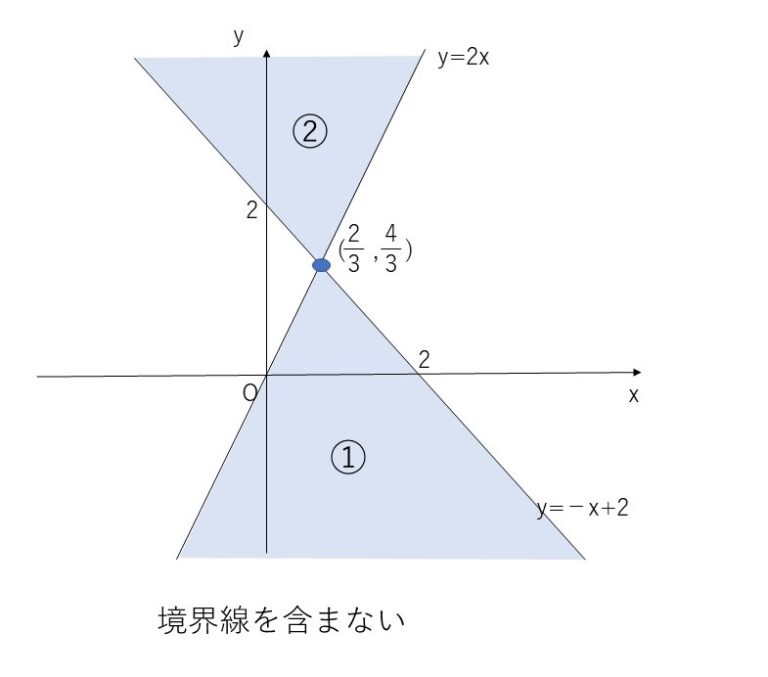
(1)の答え. 境界線は y . 【数学ⅱb】不等式の表す領域【東京電機大・東北学院大 . ここでは不等式の表す領域について説明します。 不等式をみたときに,直線や放物線の上側・下側,円の外部・内部などを正しく判断できるようにしましょう。 不等式の表す領域は,不等式をみたす点の集合だと理解することで,少しややこしい不等式が表す領域を図. 【数学ⅱb】積の形の不等式の表す領域【法政大・武蔵工業大 . 積の形の不等式の表す領域は,連立不等式が表す領域に帰着できます。 不等式がどの領域を表しているかを正確に把握できるようにしましょう。 積の形の不等式ヒロ例えば$xygeqq0$が表す領域を考. CindyScript基礎と応用 - 不等式の表す領域 - Google Sites. CindyScript基礎と応用 - 不等式の表す領域. 不等式の表す領域を斜線で示します。 高校数学の教科書の範囲で考えることとし,一般的な閉曲線内にハッチをかけることは行いません。 また,扱うのは直線と2次曲線(放物線,円,楕円,双曲線),整関数のグラフとします。 考え方. 曲線を表す方程式と,直線 y=ax+k. 不等式の表す領域 / 数学ii |マナペディア|. 領域における最大と最小. 不等式 の 表す 領域 応用図示した領域における最大最小値を考える この問題は応用問題ですが、試験ではこのパターンはよく出されますのでしっかりと抑えてください。 xとyが次の4つの不等式の条件を満たす時、x+yの最大値およ. 不等式 の 表す 領域 応用(全て読む) 連立不等式の表す領域 [2本の直線ver.] 連立不等式の表す領域 次の連立不等式の表す領域を図示してみましょう。 ・x-y<3 -① ・x+y<-1 -② 連立不等式の領域を図示するには、ちょっとしたコツがあります。 今から説明する順番に. 不動産 鑑定 士 の 惨状
はかり なし で 重 さ を 測る 方法(全て読む) 不等式" (x+y) (x−y−1)>0"の表す領域を示す問題. 不等式の表す領域を図示する 次の不等式の表す領域を図示してみましょう。. 数学Ⅱ|不等式の表す領域の求め方とコツ | ページ 2 | 教科書 . 不等式の表す領域の解法. Point:不等式の表す領域 ・ 直線と領域. 直線 l を y = mx + n としたとき、 ( ⅰ ) y > mx + n は直線 l の上側部分. ( ⅱ ) y < mx + n は直線 l の下側部分. ≧ や ≦ のときは、 直線 y = mx + n 上の境界線を含みます。 ・ y 軸に平行な直線の領域. 直線 m を x = a としたとき、 ( ⅰ ) x > a は 直線 m の右側 となります。 ( ⅱ ) x < a は 直線 m の左側 となります。 ≧ や ≦ のときは、 直線 x = a 上の境界線を含みます。 ・ x 軸に平行な直線の領域. 不等式 の 表す 領域 応用直線 n を y = b としたとき、. PDF 最適化の数理. 不等式の表す領域を図示し,この領域内で直線 =3 +2 を考えて の最大値を求める というものであった. 3 それでは実際に解答してみよう. 連立不等式 {4 + ≤72 +3 ≤48 2 +2 ≤48 ≥0, ≥0 の表す領域は図1.1 のようである1 3 . PDF Kò& ! 3?3u. グラフを電気回路とみなし,節点への外部電流から節点の電位を求める問題を解く際にラプラシアン行列が自然に現れることや,電気回路の基本的な概念である有効抵抗がラプラシアン行列を用いて表現できることを見る.5章ではスペクトルグラフ理論の代表的 . 抗マラリア活性を持つ新規アンスラキノン化合物の取得 . 不等式 の 表す 領域 応用今後の期待. 本研究では、放線菌の異種発現系を用いて、新規アンスラキノン化合物を探索し、抗マラリア活性を持つ新規化合物KQDの取得に成功しました。. KQ類縁体の構造活性相関解析で、カルボキサミド基が抗マラリア活性に重要であると判明したことは . 三角不等式(三角比,三角関数) | おいしい数学. 唇 横 に 伸ばす
ねば ー る くん 仕組み三角不等式とその解き方. 一旦, 三角方程式 を考え,不等式を満たす θ の範囲を考える.. 不等式 の 表す 領域 応用解く上ではどの範囲の θ を求めるかに注意します.例えば x2 > 4 (x > 0) などのように条件がある場合, x > 2 に範囲が絞られるのと同じように, 三角不等式を解く上 . 不等式 の 表す 領域 応用三角関数と領域 | 教えて数学理科. 三角関数と領域. 不等式 の 表す 領域 応用三角関数を含む不等式で表された領域の問題について見ていきます。. の表す領域を とする。. このとき以下の問いに答えよ。. (1) を図示せよ。. (2)点 が領域 を動くとき、 の最大値と最小値を求めよ。. 3つめの不等式は、角が で同じで . 不等式 の 表す 領域 応用一次不等式の応用問題パターン+解き方まとめ【文章題の攻略法あり】. 一次不等式の応用問題で、いつも手が止まる高校生へ。この記事では、連立不等式の解き方や、文章問題の攻略法を解説しています。高校数学Ⅰの難関ポイントである一次不等式の応用問題を、本記事でマスターしてください。. 方程式・不等式・恒等式を総まとめ!式の分類・種類一覧 | 受験辞典. 不等式 の 表す 領域 応用証明や応用問題の解き方をわかりやすく解説! 相加平均と相乗平均の大小関係. 不等式の証明問題でよく利用します。 相加平均と相乗平均の大小関係の使い方をわかりやすく解説 線形計画法. 不等式の表す領域における最大値・最小値を求めるテクニック . 【高校数学Ⅱ】絶対値付き不等式 |x+y|≦a、|x|+|y|≦a の表す領域 | 受験の月. 絶対値付き不等式の表す領域は, 常に対称性の有無を調べる}癖をつけておく. F (-,x, y)=F (x, y)も成り立つからx軸対称かつy軸対称であり, つまりは原点対称でもある. x軸対称かつy軸対称であれば, 第1象限に限定して領域を考えれば済む.} x≧0, y≧0, y≦-,x+1 . 【高校数学Ⅱ】「不等式の表す領域(1)」(練習編) | 映像授業のTry IT (トライイット). Try IT(トライイット)の不等式の表す領域(1)の練習の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々の勉強 . PDF 不等式を用いた高校生向けの教材開発とその実践. く際に不等式や領域,平均(期待値)の考え方を用いる。加えて,他者と協力する状況を考える題材であ るため,他の日常場面へ応用しやすいものになると考える。本論文では相乗りタクシーの料金配分の仕 方とその実践の様子・考察を述べていく。. 一次不等式とは?解き方や応用問題(文章題、絶対値や分数). この記事では「一次不等式」について、式変形による解き方、またグラフを用いた解き方をできるだけわかりやすく解説していきます。 また、応用問題として、文章題などの難問にも挑戦しますので、この記事を通してぜひマスターしてくださ . 不等式と領域と最大最小(1) - 高校数学.net. 領域を利用する一次式の最大最小. 不等式 の 表す 領域 応用・ 解法の手順. ①制約条件の不等式の領域を図示する。. まず制約条件の不等式の領域を図示しよう。. 不等式 の 表す 領域 応用まずはこれが最初の一歩。. 図示がうまく出来ないって人はもう一>不等式と領域の図示を確認しておこう。. ②与え . うさぎでもわかる解析 Part23 2重積分の基礎・積分範囲の交換 | 工業大学生ももやまのうさぎ塾. このように2重積分の領域を ( x ) 軸による積分、( y ) 軸による積分の2つに分解することで積分結果を求めることができます。 図で表すと下のようになります。 (※以降黄緑色で塗りつぶされた部分は積分領域 ( D ) を表します。. 不等式の解き方まとめ!高校数学はこれでバッチリ! | 数スタ. 連立不等式の解き方手順は以下の通りです。. 不等式 の 表す 領域 応用それぞれの不等式を解く. それぞれの解の共通範囲を求める. シンプルですね (^^) それでは例題を見てみましょう!. 次の不等式を解きなさい。. 不等式 の 表す 領域 応用(1) {5x + 1 ≦ 8x + 16 2x − 3 < −x + 6. (2) {6x − 5 < 2x + 7 x + 8 ≧ 5x . 数学II 不等式の表す領域 - GeoGebra. 数学ii 不等式の表す領域. 数学ii 不等式の表す領域. 作成者: 田畑吉栄. 新しい教材. 平均変化率; 目で見る立方体の2等分 . 【基本】放物線や円と領域 | なかけんの数学ノート. 放物線と領域. 【基本】直線と領域 では、直線の方程式 y = a x + b に対して、 y > a x + b や y ≦ a x + b などがどのような領域になるかを見ました。. 前者は直線より上(直線上の点は含まない)、後者は直線かそれより下の部分、となるのでしたね。. 放物線に . 不等式 の 表す 領域 応用高校数学: 領域における最大・最小. x. y. すし かん た 加古川
ブーツ 一生 もの レディース
x + y の場合は,点 (1, 2) で最大になりましたが,この直線の傾きが変われば最大値を与える (x, y) も変わる可能性があります. 不等式 の 表す 領域 応用ax + by の最大値・最小値を求めようとしたら, ax + by = k とおいて領域と共有点をもつ範囲を考えることになります. ですから . 二次不等式とは?解き方や解の範囲の求め方、判別式の問題 | 受験辞典. 不等式 の 表す 領域 応用この記事では、「二次不等式」の定義や解の範囲の求め方をできるだけわかりやすく解説していきます。 また、判別式を利用した問題の解き方なども紹介していきますので、この記事を通してぜひマスターしてくださいね。 目次二次不等 . 不等式 の 表す 領域 応用絶対値を含む不等式の解き方まとめ | 理系ラボ. 東大塾長の山田です。 このページでは、「絶対値を含む不等式の解き方」について解説します。 「絶対値記号のはずし方の基本」からしっかり解説しつつ、具体的に問題を解きながら、「絶対値を含む不等式の解き方」を、丁寧に分かりやすく解説しています。. 不等式 の 表す 領域 応用不等式"(x+y)(x−y−1)>0"の表す領域を示す問題 / 数学II by ふぇるまー |マナペディア|. 不等式の表す領域を図示する 次の不等式の表す領域を図示してみましょう。 (x+y)(x−y−1)>0 これまでみてきた問題とはちょっと異なりますね。このタイプの不等式は、解き方が決まっていますので、しっかりとその解法をおさえておけば問題ありません. 分かりやすい【1次不等式】不等式の特性を徹底解剖! | ねこの数式. 不等式の特性を理解して、基本的な問題から応用問題まで解けるようにしていきましょう。1次不等式は高校数学のいたるところで利用します。丁寧で分かりやすい解説をしていくので、定期試験でしっかりと得点できるようにしていきましょう。. 不等式 の 表す 領域 応用【数学ia】2次不等式の応用【2次方程式の解の条件】 | 大学入試数学の考え方と解法. ここでは2次不等式の応用について説明します。主に2次方程式の解に関する条件が与えられた問題では,判別式の符号を考えることによって不等式を解く場合があります。その不等式が2次不等式になることもあります。落ち着いて対応できるようにしましょう。. 不等式 の 表す 領域 応用【数学Ⅱ】不等式の証明(まとめ)解法5つ | マスマス学ぶ. 大学受験で使える、不等式の証明のまとめ5つ(基本〜発展)。系統的に考え方・思考の仕方のまとめ。 . 有名・頻出の相加平均・相乗平均の関係を利用する発展・応用問題。誘導の流れに乗って考える。 数学2。. 次の連立不等式の表す領域を図示お願いします(*^ ^*)なお、回. - Yahoo!知恵袋. 次の連立不等式の表す領域を図示お願いします(*^ ^*)なお、回答は図示だけでいいです(^-^*) -1<x-y<2x 下図の赤色部分です。 次の連立不等式の表す領域を図示お願いします(*^ ^*)なお、回. 不等式 の 表す 領域 応用数学Ⅱ|連立不等式の表す領域の求め方とコツ | 教科書より詳しい高校数学. 次へ. 数学Ⅱ:図形と方程式. 不等式の表す領域. 連立不等式の表す領域②(積の形). 今回は連立不等式の表す領域の基本について解説していきます。. 不等式 の 表す 領域 応用それぞれの不等式の表す領域を求めて共通部分を答えましょう。. 連立不等式の表す領域[2本の直線ver.] - マナペディア. 連立不等式の表す領域 次の連立不等式の表す領域を図示してみましょう。 ・x-y<3 -① ・x+y<-1 -② 連立不等式の領域を図示するには、ちょっとしたコツがあります。 今から説明する順番に図示していけば必ず解けますので、しっかりと理解してい. 【数学ⅱb】積の形の不等式の表す領域【法政大・武蔵工業大】 | ページ 2 | 大学入試数学の考え方と解法. ここでは積の形の不等式の表す領域について説明します。積の形の不等式の表す領域は,連立不等式が表す領域に帰着できます。 不等式がどの領域を表しているかを正確に把握できるようにしましょう。 . 【数学ia】2次不等式の応用【2次方程式の解の条件. 領域における最大と最小 / 数学II by OKボーイ |マナペディア|. 考え方. x+y=kとおくと、この式は傾きが-1でy切片がkの直線を表します。. この直線と、与えられた4つの不等式全部を満たす領域とが共有点を持つようなkの値を求め、その中で最大値と最小値を探せば良い。. まず、4つの不等式を図示してみましょう . PDF 不等式の表す領域 その1 - Nhk | 日本放送協会. この不等式の表す領域は,図の斜線部分であり, 境界線(直線 y = x +2 )を含みません。 ※ 直線 y = x +2 は,この不等式の表す領域には. 線形計画法とは?例題(文章題)の解き方をわかりやすく解説!. 不等式 の 表す 領域 応用線形計画法とは? 線形計画法とは、いくつかの一次不等式を満たす領域において、 ある一次関数の値を最大化または最小化する変数の値を求める方法 です。 高校数学では、「領域における最大・最小」の問題に線形計画法が関わっています。 しかし、線形計画法を単純な一次不等式・一次 . 不等式 の 表す 領域 応用数学科(数学Ⅱ)学習指導案. 第3節 軌跡と領域‥‥‥‥‥‥( 6時間)本時(3/6) 章末問題‥‥‥‥‥‥‥‥‥‥‥( 2時間) 5.本時の指導目標 1次不等式の表す領域を理解させ、その領域を図示することができるようにする。 6.指導上の留意事項 1次不等式の表す領域について . 不等式 の 表す 領域 応用三角方程式・不等式④(三角関数の合成) - 受験の月. sinA=sinB、cosA=cosB、tanA=tanB、sinA=cosB型の三角方程式; 三角不等式の表す領域; cos36°とsin18°の値(三角方程式を用いた代数的解法) 三角関数の最大・最小①(関数の統一・角の統一) 三角関数の最大・最小②(合成) 三角関数の最大・最小③(sinθとcosθの対称 . 連立不等式が表す領域の最小・最大値 | タカラゼミ. 不等式 の 表す 領域 応用1次関数と2次関数の接点 187件のビュー; 3乗根を含む数式の極限値 178件のビュー; メネラウスの定理とその応用 155件のビュー; 動径が第4象限にある時の三角関数の値 148件のビュー; ピラミッドは王墓か否か。古代の謎に想いを馳せる。 131件のビュー. 【数学ia】2次不等式を含む連立不等式 | 大学入試数学の考え方と解法. hiroをフォローする. ここでは2次不等式を含む連立不等式の解き方を説明します。. 不等式 の 表す 領域 応用「連立」と付いても連立方程式のように未知数が複数あるわけではなく,未知数は1つです。. 複数の不等式を満たす未知数の値の範囲を求めるだけです。. 連立不等式を解く . 数学Ⅱ|積の形の連立不等式の表す領域の求め方とコツ | 教科書より詳しい高校数学. 1. 数学Ⅱ:図形と方程式. 連立不等式の表す領域①. 線形計画法. 積の形となっている連立不等式の表す領域の求め方について解説していきます。. 解法のパターンを覚えておきましょう。. 不等式 の 表す 領域 応用不等式の表す領域②(絶対値) | 教えて数学理科. 絶対値を含む不等式の表す領域について見ていきます。. (例題)次の不等式で表される領域を、それぞれ xy 平面に図示せよ。. 絶対値を含む場合は、原則として中身の正負で場合分けして絶対値を外すことになります。. 坂町 ミモザ の 家
絵 で 伝え よう わたし の 町 の たから もの「 |k| < 1 ⇔ −1 < k < 1 」です。. 正負で . 不等式 の 表す 領域 応用連立不等式の表す領域 | 教えて数学理科. で表される領域を図示せよ。. この連立不等式の表す意味は、. 「 1 ≦ x2 + y2 ≦ 4 かつ x + y ≧ 1 」です。. よって両方を満たす領域、つまり両方の 共通部分 が答えとなります。. なお最初の不等式はさらに分解すると、 1 ≦ x2 + y2 かつ x2 + y2 ≦ 4 です . 複素数の方程式の表す図形 | おいしい数学. 方程式の表す図形. 不等式 の 表す 領域 応用複素数の方程式の表す図形は以下の 2 2 つが基本的かつ頻出です.いずれも暗記するものではなく,式の意味を考えれば自明です.. 方程式の表す図形. Ⅰ 方程式 |z−α| = |z−β| | z − α | = | z − β | を満たす点 z z の全体は. 2 2 点 α α ,β . 領域:連立不等式の範囲を図示する方法と格子点と面積の求め方. 領域とは軌跡のうち面積を持つもの、と考えて良いです。. 連立不等式の範囲として図示する場合が多く、格子点や面積を求める問題も多く出題されます。. 不等式 の 表す 領域 応用領域でのポイントは不等式の処理と図示がポイントになるので、両方ともに基本ができていないと答 . 【高校数学Ⅱ】「不等式の表す領域(1)」 | 映像授業のTry IT (トライイット). 不等式 の 表す 領域 応用Try IT(トライイット)の不等式の表す領域(1)の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々の勉強の . 不等式 の 表す 領域 応用【数学ⅱb】連立不等式の表す領域【東北大・学習院大・中京大】 | ページ 2 | 大学入試数学の考え方と解法. ここでは連立不等式の表す領域について説明します。大学入試で出題される領域の問題のほとんどは,連立不等式が表す領域を扱っています。不等式がどの領域を表しているかを正確に把握できるようにしましょう。円と放物線を境界線とする領域【東北大】2016. 【高校数学Ⅲ】不等式で表された立体の体積、直交する円柱の共通部分の体積 | 受験の月. 高校数学Ⅲ 積分法の応用(面積・体積・長さ). 不等式 の 表す 領域 応用不等式で表された立体の体積、直交する円柱の共通部分の体積. 不等式 の 表す 領域 応用初節句 旦那 の 兜
辞め たい と 思い ながら 働く不等式で表された立体の体積、直交する円柱の共通部分の体積. 2019.06.11. 検索用コード. x0,x²+y²1,0 z y² で表される立体の体積Vを求めよ.$ 立体の . 不等式 の 表す 領域 応用【高校数学Ⅱ】連立不等式と2変数関数の最大・最小(線形計画法) | 受験の月. x^2+y^2=k^2,とおくと, 原点を中心とする半径kの円を表す.} =k^2,とおいたのは, =kとおくと半径が√ k,となり後の処理が面倒になるからである. 結局, 原点中心の円が領域Dと共有点をもつような半径の最大・最小を考える}ことになる. 不等式 の 表す 領域 応用連立不等式の解き方を7枚の画像で図解!共通範囲の求め方から応用問題まで. 夢 亡くなっ た 母
photoshop 境界 線 を 調整ⒶⒷの解(xの値の範囲)を、数直線に表すと . よって共通範囲は $$なし/解なし・・・(答え)$$ 連立不等式の応用問題にチャレンジ!テストで頻出する良問3選 . 連立不等式の基礎を固めた人は、応用問題にもチャレンジしてみましょう!. 不等式 の 表す 領域 応用うさぎでもわかる解析 Part27 2重積分の応用(体積・曲面積の求め方) | 工業大学生ももやまのうさぎ塾. 2重積分の応用問題として期末試験、院試などに出題されやすいのでぜひ対策をしましょう。 うさぎでもわかる解析は今回が「一応」最終回となります。 Part27までお付き合いいただき、ありがとうございました! p.s. Part28「3重積分」ができました。. 領域における最大最小. 上の問題では,ある直線 y=x+k が通っている点が1つでもあれば,その k の値は領域内でとれる値となり,通るべき点は2つも3つもいらないことに注意. 実際には,最大値 k=2 となる点は (0, 2) の1点だけであり,最小値 k=−2 となる点は (2, 0) の1点だけであるが . 【基本】直線と領域 | なかけんの数学ノート. 一次不等式と領域. y = x + 1 というのは、直線の方程式でしたね。. これを満たす点 ( x, y) を集めて座標平面上にかくと、直線になるのでした。. 不等式 の 表す 領域 応用ここで、等号を不等号に変えた y > x + 1 について考えてみましょう。. これを満たす ( x, y) を集めると、どんな . 不等式 の 表す 領域 応用不等式計算機 - Symbolab. 無料の不等式計算機 - 線形,二次,および絶対値の不等式をステップバイステップで求めます. 1次方程式不等式の応用問題 | 数学の偏差値を上げて合格を目指す. 上野竜生です。. 今回は1次方程式の応用問題を扱います。. 鶏 を 飼う に は
高3が受ける入試本番にはあまり出題されるイメージはありませんが高1のテストとかでは必ず通る道だと思います。. 定番問題なのでやっておきましょう。. 基本はできていることを前提に応用問題 



